适用边界：真理存在吗？

作者|兰陵王   来源|学习有了方法（ID：xuexiyoulefangfa）

菲茨杰拉德：同时保有两种截然相反的观念还能正常行事，是一流智慧的标志。

两年前，马云说了这样一段话：

关于996，现在是国内的一个很热门的话题，很多企业都有这个问题。我个人认为，能做996是一种巨大的福气，很多公司、很多人想996都没有机会。如果你年轻的时候不996，你什么时候可以996？你一辈子没有996，你觉得你就很骄傲了？

这个世界上，我们每一个人都希望成功，都希望美好生活，都希望被尊重，我请问大家，你不付出超越别人的努力和时间，你怎么能够实现你想要的成功？

在网上被骂成狗。

后来，蚂蚁金服即将上市的消息传来……

阿里的员工彻底沸腾了，整栋楼都是财务自由的欢呼声。

▲《华尔街之狼》

据估计，蚂蚁金服估值将达到2000亿美元，折合人民币大约15000亿。根据股权架构，至少有将近60位高管及合伙人将成为亿万富翁，最低身价达6.65亿。

至于千万富翁，简直是直接批量生产……有人做了一笔计算，假设蚂蚁金服有10万员工，按阿里系83%的持股，即使均分的话每人也能分得1245万。

然后网上好多人又开始酸了……觉得996的福报来了。

你看，人们在面对同一个道理的时候，居然会呈现两种截然不同的反应。

一会觉得“996福报”是资本主义的丑恶嘴脸；一会又开始酸了，觉得我为什么不是阿里的员工？

真奇怪，是什么原因导致了这样的现象？

答案是：几乎99%的人都不知道，每个道理都有它的适用边界。

这是非常重要的一个思维模型「适用边界」。

老实说，这个思维模型我是最近两年才深刻意识到的，它源自两本书《模型思维》和《结构化思维》。

《模型思维》和《结构化思维》的作者都在书中反复强调说，每个思维模型都有“适用边界”，一切避开“适用边界”谈思维模型的行为都是耍流氓。

看得我大受震动。

过去我一直都在用思维模型指导行事，但是我居然从来没有认真的去思考过它们的适用边界。

实在惭愧。

遂立马把它迭代进模型树，作为模型树很重要的一环。

之所以写这篇文章，也是希望它能迭代进你们的模型树，或者完善你们的每一个思维模型。

世界上有真理吗？？？

一直以来，无数的哲学家、数学家、科学家、逻辑学家都在追求得到一个绝对正确的真理。

因为无论什么科学体系，亦或者是哲学和数学，其出发点都建立在一些不证自明的公理上，然后靠演绎去推导。

所以，出发点是否为真至关重要。

然而那些不证自明的公理，真的是真理吗？？？

这似乎只能求助于我们的直观，那些直观上非常简单，甚至根本无法想象它不对的命题就能作为公理。

比如欧式几何的五条公理之一：过相异两点，能作且只能作一直线。

但是人们逐渐发现，靠直观的公理还是可能会错。比如，集合论公理也会自相矛盾，最著名的就是罗素悖论。

于是后来出现了一位大数学家希尔伯特，他向全世界的数学家抛出一个宏伟的计划，希望建立一套公理体系，使一切数学命题都可以经此判定真伪。这叫做“公理体系的完备性”。

然而，正当这个宏伟的计划在有序推进，几乎全世界的数学家都期待着数学大厦即将竣工的时候。

一道晴天霹雳打在了希尔伯特等数学家的头上，哥德尔带着他的不完备性定理出现了。

一、伟大的哥德尔

哥德尔是谁？

他是20世纪最伟大的数学家和逻辑学家。

爱因斯坦曾评价哥德尔对数学的贡献可以匹敌自己对物理学的贡献。

哈佛大学授予哥德尔荣誉学位的时候，曾高度评价哥德尔，称其为“20世纪最有意义的数学真理发现者”。

哥德尔的晚年好友王浩（逻辑学家），曾将他的贡献，同弗洛依德的心理学、爱因斯坦的相对论、玻尔的互补性原理、海森堡的测不准原理、凯恩斯的经济学、沃森和克里克的DNA双螺旋结构，并称为“20世纪人类思想史上的奠基性贡献”。

美国《时代》杂志曾评选出20世纪100个最伟大的人物，在数学家中，排在第一的就是哥德尔。

二、伟大的哥德尔不完备性定理

1931年哥德尔提出了不完备性定理，那年他年仅25岁。

这一理论对数学产生了划时代的影响，也成为逻辑学的丰碑。

代表着西方最顶级的理性思潮，是西方自古以来理性思维的高峰。

以往大多数数学家都认为，如果某个命题是正确的，就一定可以用数学演绎的方法证明其为真；如果某个命题是错误的，也一定可以用数学演绎的方法证明其为假。

典型的代表就是庞加莱，他认为只要我们拟定了定义和公理之后，一个定理就只能为真或为假。

然而哥德尔不完备性定理却发现，在任何一个包含皮亚诺算术的形式系统中，必定包含一些命题，既不能用系统中的公理和推理规则证明其为真，也不能用系统中的公理和推理规则证明其为假。

翻译一下就是：在任何一个表达力足够、推理能力足够的形式系统中，必定包含一些命题，既不能被证明为真，也不能被证明为假。

即，命题自身无法在此公理体系内被证明。

我们根本无法确定真理的存在。

当然，这句话也是有适用边界的。

它仅仅是针对数学领域而言，而且是针对表达力足够、推理能力足够的形式系统。

哥德尔本身也极为谨慎，不愿意把这条定理扩散到数学以外的领域。

比如老子所说的“道生一，一生二，二生三，三生万物”就无法用哥德尔不完备性定理去驳斥。除非我们可以把它转为为形式系统，并且能够用哥德尔的证明方法去证明。

三、哥德尔不完备性定理对其他领域的影响

虽然哥德尔本身排斥把这条定理扩散到数学以外的领域。

但是它确实是给整个世界带来了震动和启迪。

哥德尔不完备定理不仅直接对逻辑学和数学产生了空前的影响，而且还延伸到其余的领域，比如计算机、哲学、心脑科学、认知科学等领域，都产生了非常大的影响。——罗西. 哥德尔定理及其方法论意义[D].浙江大学,2015.

因为这些领域虽然不像数学那样形式化，但是思维方式却是一样的。都是从一些不证自明的公理出发，然后用演绎去推导。

最终大家都逃不过一个命题——这些不证自明的公理是否绝对为真？

后来塔尔斯基（哲学家、逻辑学家、语言学家），用形式语言去证明哲学领域的真理，最后也得出类似的结论，即一个给定语言的句子的真理概念不能在这个语言内被一致性的定义出来。

这就是著名的塔尔斯基不可定义性定理。

对于物理学领域，著名的宇宙学家霍金先生，在国际弦理论会议上发表了题为《哥德尔与M理论》的报告，认为建立一个单一的描述宇宙的大统一理论是不太可能的，这一推测也是基于哥德尔不完全性定理。

虽然哥德尔不完备定理是针对数学而提出的，但是它的光芒拂照着理性大地。

就我个人而言，这几天看了很多相关的论文，整个人好像蜕变了似的。

变得更加谦卑和理性了。

连数学这门严格以不证自明的公理为起点，然后再演绎推理的学科，这么追求从真到真的学科，都尚且无法证明真理的存在。

我们平时用归纳法总结的道理，从别人那里听来的道理，恐怕也得谦卑一点吧？

至少在证明它为真理之前，加上一个适用边界并不过分。

每个思维模型都有它的适用边界

什么是适用边界？

适用边界建立在一条谦卑的心态之上，即「我现在所吸收到的道理都不是绝对的真理，它们只在某些特定的条件下、某些特定的场合下适用」。

为什么马云说996是福报会被骂成狗？

因为在大多数人眼中，只有简单的是非对错。一个道理要么是对，要么就是错。

可是这个世界并不是简单的黑白分明。

如果我们以如此简单的对错去判定一个道理，也难怪会懂了那么多道理却依旧过不好这一生了。

聪明的人，是能够同时保有两种截然不同的观念，还能正确行事，这是一流智慧的标志。——菲茨杰拉德

很长一段时间我不懂菲茨杰拉德的这句话到底是什么意思。

直到后来我在《模型思维》和《结构化思维》这两本书中看到“适用边界”这个思维模型的时候，立刻恍然大悟。

没有正确的思维模型，只有适合某种情况的思维模型。——《好好思考》

我们需要划出一条界线：什么时候应该采用，什么时候不能采用。——《模型思维》

没有能够适应所有场景下的概念、方法和套路……它们都只能在一定的有效范围内使用，这就是适用边界。——《结构化思维》

比如下面这些古老的道理：

古人说：不见棺材不落泪

古人说：车到山前必有路

古人说：坚持就是胜利

古人说：苦海无涯回头是岸

古人说：英雄出少年

古人说：大器晚成

古人说：小心驶得万年船

古人说：富贵险中求

古人说：宁为玉碎不为瓦全

古人说：留得青山在不怕没柴烧

什么感受？

不看另外一句话，觉得卧槽，好有道理；看了另一句话，觉得卧槽，我到底该相信哪个？

之所以会这样，是因为我们心里没有“适用边界”这个思维模型。

于是就会用非常简单的是非对错去判定一个道理，要么一棍子打死，要么就全盘接受。

最后的结局就是「听过那么多道理，却依然过不好这一生」。

千万不要这样，每个思维模型都有它的适用边界。

几乎没有一个道理是全对的，也几乎没有一个道理可以适用于所有场景。正如统计学家乔治·博克斯所说的：

所有模型都是错的，但有些模型是有用的。——乔治·博克斯

所以，你要学会分辨，看看它们的适用边界在哪里，哪些场景适用，哪些场景不适用。

择其善者而用之。

比如我上一个思维模型“检索练习”，有些读者看了就立马反驳说：

▲只看到事物的表象

▲心智固化，拒绝接受新知识

▲固定型思维，居然这么多人点赞

检索练习确实不是对所有学习都适用，比如你要背100串数字，那可能记忆宫殿、联想法、挂钩法更适合。

关键我也没说它是真理啊。

事实上我经常在读者群里反复提醒大家，要独立思考，几乎每个思维模型都有它的适用边界和适用场景。

不要给自己加戏好吗？

回到主题，如果你懂了适用边界，菲茨杰拉德那句话就好理解了。

菲茨杰拉德所说的“两种截然不同的观念”，比如上面那些古人说的话，像是“小心驶得万年船”与“富贵险中求”。

意思是，你要懂得去分辨，这两个道理的适用边界在哪里，哪些场景下使用“小心使得万年船”，哪些场景下使用“富贵险中求”。

做到这点，就能够同时保有两种截然不同的观念，还能正确行事。

画个图你就懂了。

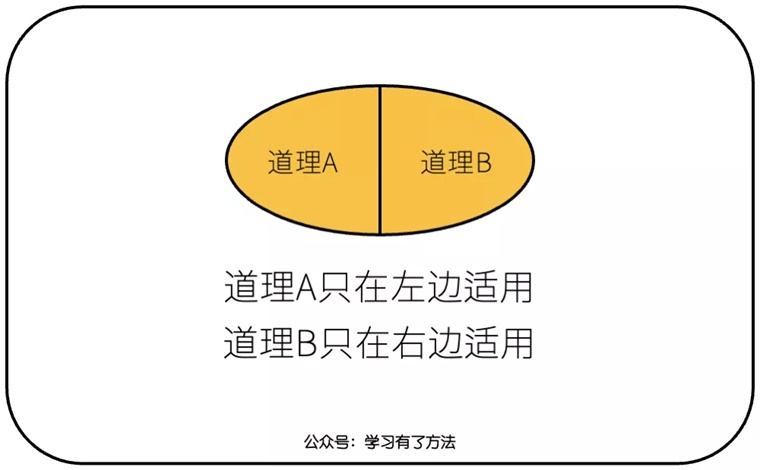
道理A与道理B是截然相反的两个道理，左边是道理A的适用边界，右边是道理B的适用边界。

只要你在各自的适用边界内使用各自的道理，就能正确行事。

然而大多数人却认为这个世界是非黑即白的，要么A正确，要么B正确。

像极了哥德尔不完备性定理提出之前，很多数学家都认为，一个命题要么为真，要么就为假。

适用边界对思维模型的启示

一开始我解释一个思维模型用的是经典的认知圈思维，即「是什么、为什么、怎么做」。

顶多再加上一个注意事项。

自从懂了适用边界之后，我的框架里面就多了一个东西，叫做适用边界。

比如哥德尔不完备性定理，它的适用边界是：数学领域、形式系统、皮亚诺算术。

当然，这个适用边界是巨人告诉我们的，实际生活中很多思维模型是我们自己提炼出来的，根本没人告诉我们适用边界怎么办呢？

或者像“小心驶得万年船”和“富贵险中求”这种前人传下来的道理，我们根本不知道它的适用边界怎么办呢？

我的做法是退一步，先不忙着给出清晰的适用边界，先去试错，沉淀出几个经典案例，然后根据经典案例归纳出适用场景。

有了经典案例，有了适用场景，就可以寻找它们的共性，慢慢沉淀出精确的适用边界。

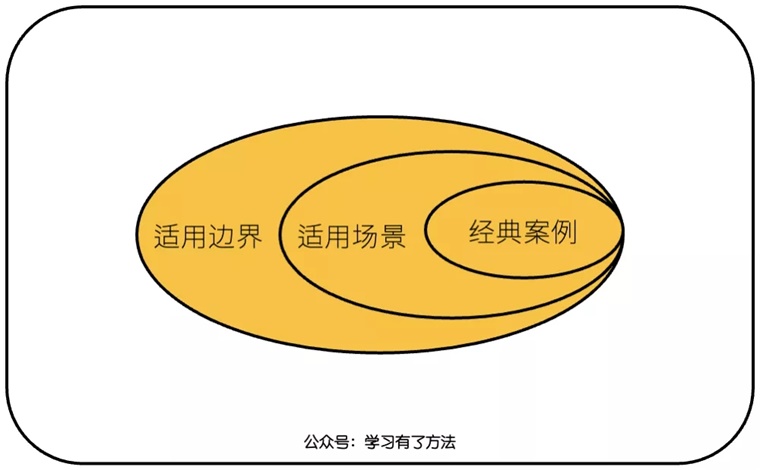
这也是成甲在书中说的，学到一个思维模型要不断去思考，这个思维模型可以被用到哪些经典场景……

其目的也是为了寻找这个思维模型的适用边界。

最后，我们来聊一聊批判性思维吧。最近看到汤质的文章，有些感触。

大多数人眼中的批判性思维其实是：

某个观点错了——这个人的所有观点大概也错 

某个人是权威——这个人大概率是对的 

某个人站在了权威的对立面——他大概率是错的 

尤其是第一点，好多人喜欢用「局部错意味着整体错」，来反对一切自己不喜欢的观念。

可是读完这期的文章你就知道，这世上几乎没有真理。

也就是说，几乎所有道理，所有思维模型，都有错误的部分，都有不适用的场景。

如果你一直秉承「局部错意味着整体错」的观念，那你就拒绝了一切成长的可能。

老规矩，最后送给大家一句我很喜欢的话，也是我个人的处世原则和学知识的原则。

我只看你万般好，其他不好我不看。

编者按：本文转载自微信公众号：学习有了方法（ID：xuexiyoulefangfa），作者： 兰陵王